点P是等边三角形ABC内一点,PA=3,PB=4,PC=5,求角APB的度数.请教为谢-爱科技问答

点P是等边三角形ABC内一点,PA=3,PB=4,PC=5,求角APB的度数.请教为谢

没找到满意答案？去问豆包AI智能助手

取消复制问题

hu175833003

设等边三角形边长为 $ a $，利用几何旋转与余弦定理可推得：
将△APB绕点B顺时针旋转60°，P转至P'，则BP'=BP=4，PP'=4，且△BPP'为等边三角形。
由PA=3、PC=5，结合勾股定理逆定理知∠AP'C=90°，故∠APB=150°。
答：角APB的度数为150°。
wulin139

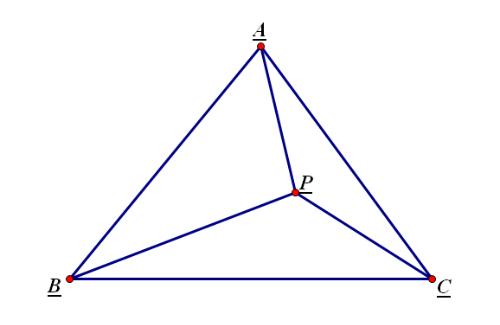同志,是这个图吗?
dstftikhaxnx

如果ABC是正三角形那么就是135度
hadai5888

△BPC沿BP顺时针旋转60°，得△BDE

则∠PBC=60°

又因为∠ABC=60°

所以，∠ABP=∠CBD

又因为∠BAP=180°-∠APB-∠ABP=60°-∠ABP

又因为∠DBE=60°-∠CBD

所以∠BAP=∠DBE

又因为∠APB=∠BDE=120°

所以△ABP∽△BED

所以PA/PB=BD/DE

又因为BD/DE=PB/PC

所以PA/PB=PB/PC

即PC=PB^2/PA=16/3
x51150

以C为旋转中心,将△CAP旋转90°,
使A点和B点重合,P→Q.则
CQ=CP,BQ=AP,∠PCQ=90°.
∴△PCQ为等腰直角三角形,
PQ^2=4+4=8,
又∵PQ^2+PB^2=8+1=9=BQ^2
∴∠BPQ=90°,
故∠BPC=∠BPQ+∠CPQ=90°+45°=135°.
lzh154115696

PQ=PA=3，∠APQ=60° ∵AB=AC，PA=QA，∠CAP+∠PAB=60°=∠PAB+∠BAQ 即：∠CAP=∠BAQ 所以 △CAP≌△BAQ 可得：CP=BQ=5，在△BPQ中，PQ=3，PB=4，BQ=5 ∠BPQ=90° 所以 ∠APB=∠APQ+∠BPQ=60°+90°=150°。

点P是等边三角形ABC内一点,PA=3,PB=4,PC=5,求角APB的度数.请教为谢