标准差是用来衡量数据分散程度的指标。它表示一组数据中每个数据值与平均值的差异程度。标准差越大,说明这组数据分布越广,离平均值越远;标准差越小,说明这组数据分布越集中,离平均值越近。
在统计学中,我们经常使用标准差来评估数据的可靠性。如果一个样本的标准差很大,则可以推断出这个样本中的数据可能存在异常值;而如果一个总体(或总体中某个子集)的标准差很小,则说明该总体(或子集)中的数据具有高度一致性。
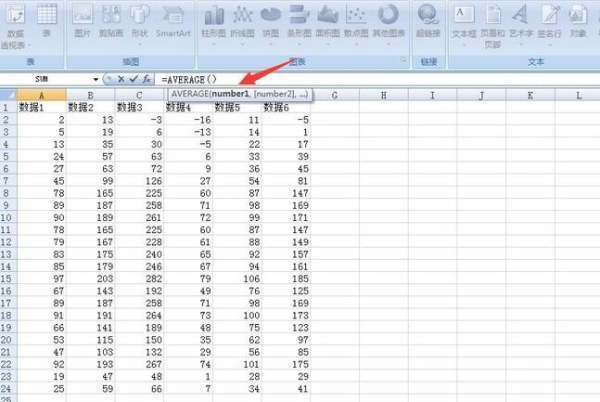
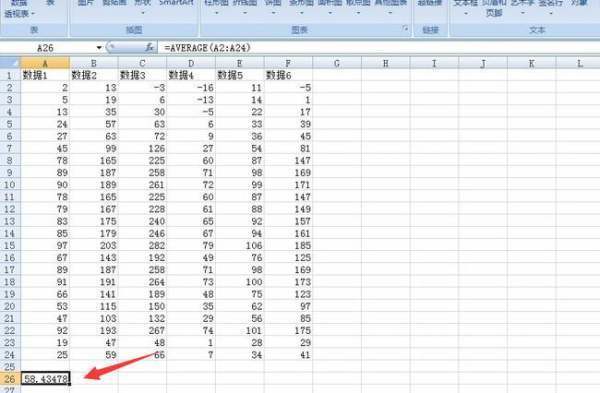
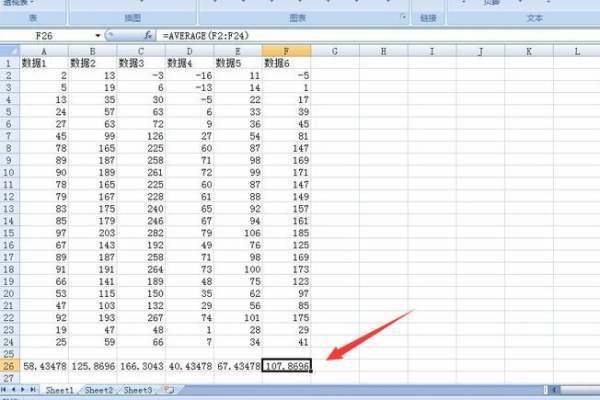
需要注意的是,在计算标准差时必须先计算出平均值。对于一个含有N个元素的样本,其计算公式为:
标准差 = sqrt(((x1 - x mean)^2 + (x2 - x mean)^2 + ... + (xn - x mean)^2) / (N-1))
其中x1、x2、xn为样本中的数据值;x mean为样本平均值;N为样本个数。
总结起来就是:标准差越大,说明这组数据分布越广,离平均值越远;标准差越小,说明这组数据分布越集中,离平均值越近。在使用标准差时需要先计算出平均值,并注意其中的公式和注意事项。
在统计学中,我们经常使用标准差来评估数据的可靠性。如果一个样本的标准差很大,则可以推断出这个样本中的数据可能存在异常值;而如果一个总体(或总体中某个子集)的标准差很小,则说明该总体(或子集)中的数据具有高度一致性。
需要注意的是,在计算标准差时必须先计算出平均值。对于一个含有N个元素的样本,其计算公式为:
标准差 = sqrt(((x1 - x mean)^2 + (x2 - x mean)^2 + ... + (xn - x mean)^2) / (N-1))
其中x1、x2、xn为样本中的数据值;x mean为样本平均值;N为样本个数。
总结起来就是:标准差越大,说明这组数据分布越广,离平均值越远;标准差越小,说明这组数据分布越集中,离平均值越近。在使用标准差时需要先计算出平均值,并注意其中的公式和注意事项。